Bayesian Methods

Introduction

Bayesian inference is a statistical approach based on Bayes’ theorem, which describes how to update beliefs based on new evidence. This approach provides a framework for reasoning about probabilities in the presence of uncertainty.

Bayes’ theorem states that:

$$P(H | E) = \frac{P(E | H) P(H)}{P(E)}$$

where:

• $P(H | E)$ is the posterior probability of hypothesis $H$ given evidence $E$.
• $P(E | H)$ is the likelihood of observing evidence $E$ given that hypothesis $H$ is true.
• $P(H)$ is the prior probability of hypothesis $H$ before observing evidence $E$.
• $P(E)$ is the probability of evidence $E$ occurring.

This document explores Bayesian methods for risk probability and cost probability density estimation.

Inference for Risk Probability

Consider a risk event $R$ that may be caused by multiple root causes $C_1, C_2, \dots, C_n$. The probability of $R$ occurring can be computed as:

$$P(R) = \sum_{i=1}^{n} P(R | C_i) P(C_i) + P(R | \neg C_i) P(\neg C_i)$$

where:

• $P(R | C_i)$ represents the probability of $R$ occurring given that $C_i$ is present.
• $P(C_i)$ is the prior probability of the root cause $C_i$.
• $P(R | \neg C_i)$ is the probability of $R$ occurring when $C_i$ is absent.
• $P(\neg C_i) = 1 - P(C_i)$ is the probability that $C_i$ does not occur.

The function risk_prob calculates the probability of the risk event given the root causes and their conditional probabilities.

Example

First, load the package:

library(PRA)

Suppose there are two root causes with probabilities $P(C_1) = 0.3$ and $P(C_2) = 0.2$.

cause_probs <- c(0.3, 0.2)

The conditional probabilities of the risk event given each cause are $P(R | C_1) = 0.8$ and $P(R | C_2) = 0.6$, respectively. The conditional probabilities of the risk event given not each cause are $P(R | \neg C_1) = 0.2$ and $P(R | \neg C_2) = 0.4$.

risks_given_causes <- c(0.8, 0.6)
risks_given_not_causes <- c(0.2, 0.4)

To calculate the probability of the risk event, use the risk_prob function:

risk_prob_value <- risk_prob(cause_probs, risks_given_causes, risks_given_not_causes)
cat(risk_prob_value)

0.82

Inference for Cost Probability Density

The cost_pdf function uses Bayesian inference to model the probability distribution of cost outcomes based on the occurrence of risk events. It assumes that each risk event contributes to the total cost according to a normal distribution, leading to a mixture model representation:

$$P(A) = \sum_{i=1}^{n} P(R_i) \cdot N(A | \mu_i, \sigma_i) + P(\neg R_i) \cdot N(A | \text{base_cost}, 0)$$

where:

• $P(R_i)$ is the probability of risk event $R_i$.
• $N(A | \mu_i, \sigma_i)$ is the normal distribution with mean $\mu_i$ and standard deviation $\sigma_i$.
• $P(\neg R_i) = 1 - P(R_i)$ is the probability that risk event $R_i$ does not occur.
• $N(A | \text{base_cost}, 0)$ is a point mass at the baseline cost $\text{base_cost}$.

The function cost_pdf generates random samples from the mixture model to estimate the cost distribution.

Example

Suppose there are three risk events with probabilities $P(R_1) = 0.3$, $P(R_2) = 0.5$, and $P(R_3) = 0.2$.

risk_probs <- c(0.3, 0.5, 0.2)

The means and standard deviations of the normal distributions for cost given each risk event are:

means_given_risks <- c(10000, 15000, 5000)
sds_given_risks <- c(2000, 1000, 1000)

The baseline cost is $\text{base_cost} = 2000$.

base_cost <- 2000

To generate random samples from the cost distribution, use the cost_pdf function:

num_sims <- 1000
samples <- cost_pdf(num_sims, risk_probs, means_given_risks, sds_given_risks, base_cost)
hist(samples, breaks = 30, col = "skyblue", main = "Histogram of Cost", xlab = "Cost")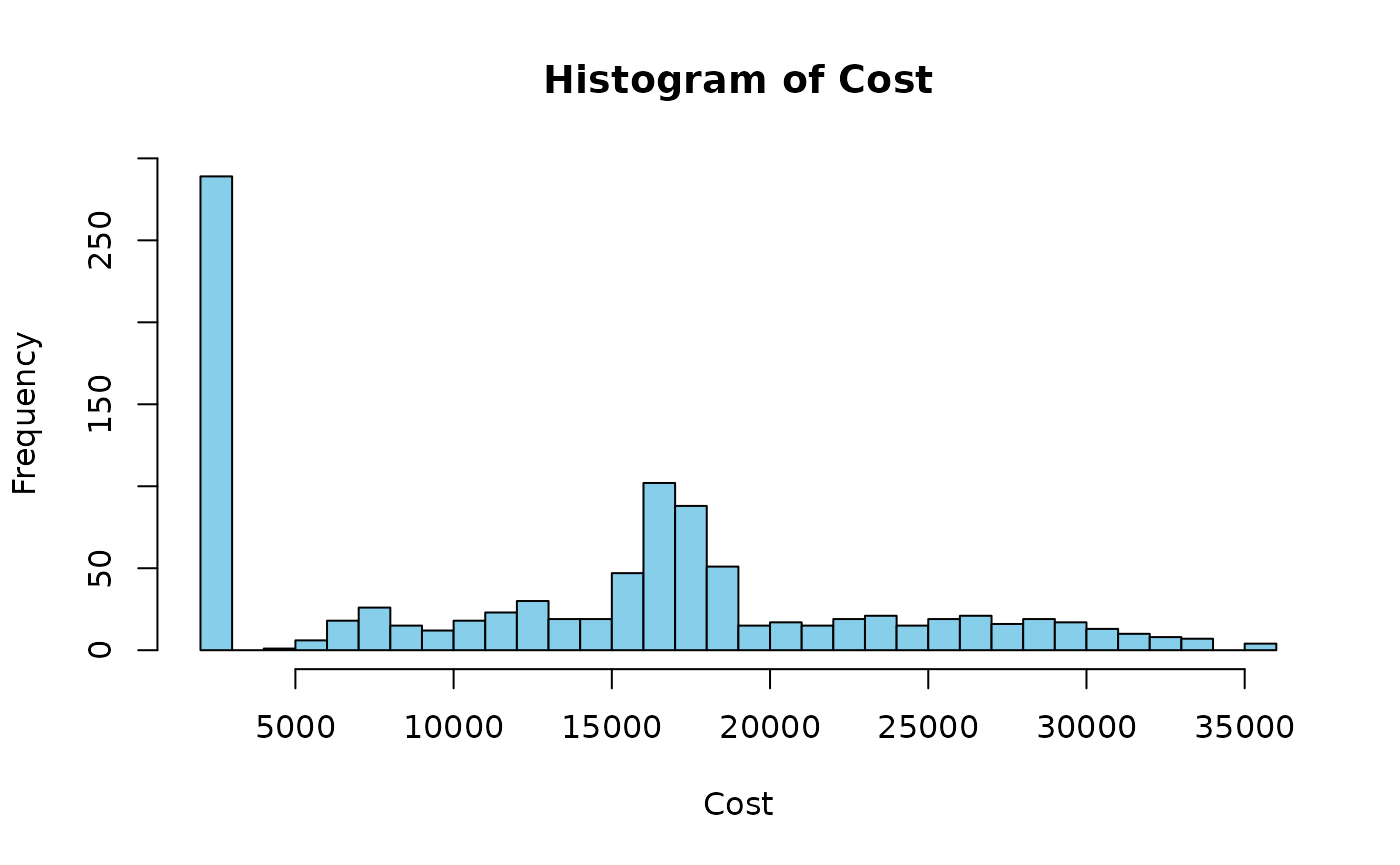

The histogram above shows the distribution of cost outcomes based on the risk events and their associated costs.

Posterior Risk Probability

Bayesian updating is the process of updating prior beliefs given new evidence. The risk_post_prob function calculates the posterior probability of a risk event given observations of its root causes. This is achieved by applying Bayes’ theorem to update the prior probabilities of root causes based on the observed data.

Example

Suppose there are two root causes with prior probabilities $P(C_1) = 0.3$ and $P(C_2) = 0.2$.

cause_probs <- c(0.3, 0.2)

The conditional probabilities of the risk event given each cause are $P(R | C_1) = 0.8$ and $P(R | C_2) = 0.6$, respectively. The conditional probabilities of the risk event given not each cause are $P(R | \neg C_1) = 0.2$ and $P(R | \neg C_2) = 0.4$.

risks_given_causes <- c(0.8, 0.6)
risks_given_not_causes <- c(0.2, 0.4)

Suppose the observed root causes are $C_1 = 1$ and $C_2 = \text{NA}$.

observed_causes <- c(1, NA)

To calculate the posterior probability of the risk event, use the risk_post_prob function:

risk_post_prob <- risk_post_prob(cause_probs, risks_given_causes,
  risks_given_not_causes, observed_causes)
cat(risk_post_prob)

0.6315789

The posterior probability of the risk event is updated based on the observed root causes.

Posterior Cost Probability Density

The cost_post_pdf function generates a posterior probability density function (PDF) for costs, given observed risk events. This function simulates random samples from a mixture model based on Bayesian updating principles.

Example

Suppose there are three risk events with observed values $R_1 = 1$, $R_2 = \text{NA}$, and $R_3 = 1$.

observed_risks <- c(1, NA, 1)

The means and standard deviations of the normal distributions for cost given each risk event are:

means_given_risks <- c(10000, 15000, 5000)
sds_given_risks <- c(2000, 1000, 1000)

The baseline cost is $\text{base_cost} = 2000$.

base_cost <- 2000

To generate random samples from the posterior cost distribution, use the cost_post_pdf function:

num_sims <- 1000
posterior_samples <- cost_post_pdf(
  num_sims = num_sims,
  observed_risks = observed_risks,
  means_given_risks = means_given_risks,
  sds_given_risks = sds_given_risks,
  base_cost = base_cost
)

hist(posterior_samples, breaks = 30, col = "skyblue", main = "Posterior Cost PDF", xlab = "Cost")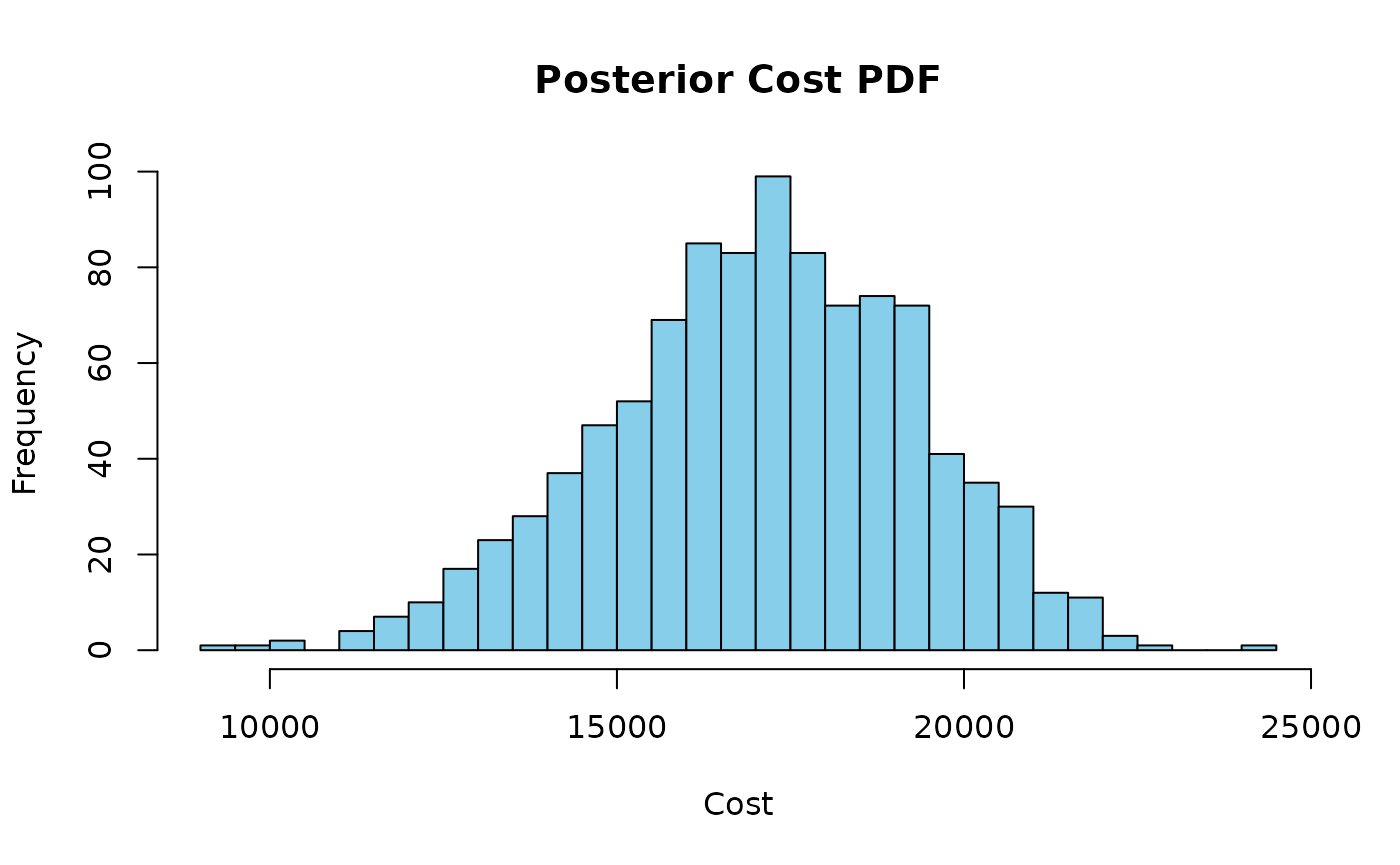

The histogram above shows the posterior probability density function of costs based on the observed risk events.

Conclusion

Bayesian methods provide a powerful framework for updating beliefs and making inferences based on observed data. By incorporating prior knowledge and new evidence, these methods can help quantify uncertainty and make informed decisions in a wide range of applications.