Skip to contents

Earned Value Management

Source: vignettes/evm.Rmd
evm.Rmd

Earned Value Management (EVM) is a project management technique used to measure project performance and progress in an objective manner. It integrates project scope, time (schedule), and cost parameters to provide accurate forecasts of project performance issues.

Key Components

  1. Budget at Completion (BAC): The total budget for the project.
  2. Actual Cost (AC): The cumulative actual cost incurred for the work performed to date.
  3. Planned Value (PV): The authorized budget assigned to scheduled work.

PV=BAC*PlannedPercentCompletePV = BAC * PlannedPercentComplete

  1. Earned Value (EV): The value of work actually performed expressed in terms of the approved budget for that work.

EV=BAC*ActualPercentCompleteEV = BAC * ActualPercentComplete

Common EVM Equations

  1. Cost Variance (CV): Positive CV indicates under budget and negative CV indicates over budget.

    CV=EV−ACCV = EV - AC

  2. Schedule Variance (SV): Positive SV indicates ahead of schedule and negative SV indicates behind schedule.

    SV=EV−PVSV = EV - PV

  3. Cost Performance Index (CPI): CPI > 1 indicates cost efficiency and CPI < 1 indicates cost inefficiency.

    CPI=EVACCPI = \frac{EV}{AC}

  4. Schedule Performance Index (SPI): SPI > 1 indicates schedule efficiency and SPI < 1 indicates schedule inefficiency.

    SPI=EVPVSPI = \frac{EV}{PV}

  5. Estimate at Completion (EAC): Multiple methods available:

    • Typical: EAC=BACCPIEAC = \frac{BAC}{CPI} (assumes current performance continues)
    • Atypical: EAC=AC+(BAC−EV)EAC = AC + (BAC - EV) (assumes future work at planned rate)
    • Combined: EAC=AC+BAC−EVCPI×SPIEAC = AC + \frac{BAC - EV}{CPI \times SPI} (considers both cost and schedule)

  6. Estimate to Complete (ETC): Expected cost to finish remaining work.

    ETC=BAC−EVCPIETC = \frac{BAC - EV}{CPI}

  7. Variance at Completion (VAC): Expected budget variance at project end.

    VAC=BAC−EACVAC = BAC - EAC

  8. To-Complete Performance Index (TCPI): Required efficiency on remaining work.

    TCPI=BAC−EVBAC−ACTCPI = \frac{BAC - EV}{BAC - AC}

Examples

First, load the package:

library(PRA)
#> Registered S3 method overwritten by 'PRA':
#>   method    from 
#>   print.nls stats

Then set the BAC, schedule, and current time period for a toy project.

bac <- 100000
schedule <- c(0.1, 0.2, 0.4, 0.7, 1.0)
time_period <- 3

Calculate the PV and print the results:

pv <- pv(bac, schedule, time_period)
cat("Planned Value (PV):", pv, "\n")

Planned Value (PV): 40000

Set the actual % complete and calculate the EV:

actual_per_complete <- 0.35
ev <- ev(bac, actual_per_complete)
cat("Earned Value (EV):", ev, "\n")

Earned Value (EV): 35000

Set the actual period costs and calculate the cumulative AC to date:

# Period costs (cost incurred each period)
period_costs <- c(9000, 18000, 36000)

# Calculate cumulative AC using cumulative = FALSE
ac <- ac(period_costs, time_period, cumulative = FALSE)
cat("Actual Cost (AC):", ac, "\n")

Actual Cost (AC): 63000

Calculate the SV and CV and print the results:

sv <- sv(ev, pv)
cat("The project is behind schedule because the Schedule Variance (SV) is", sv, "\n")

The project is behind schedule because the Schedule Variance (SV) is -5000


cv <- cv(ev, ac)
cat("The project is over budget because the Cost Variance (CV) is", cv, "\n")

The project is over budget because the Cost Variance (CV) is -28000

Calculate the SPI and CPI and print the results:

spi <- spi(ev, pv)
cat("The project is behind schedule because the Schedule Performance Index (SPI) is", round(spi, 2), "\n")

The project is behind schedule because the Schedule Performance Index (SPI) is 0.88


cpi <- cpi(ev, ac)
cat("The project is over budget because the Cost Performance Index (CPI) is", round(cpi, 2), "\n")

The project is over budget because the Cost Performance Index (CPI) is 0.56

Calculate the EAC using different methods:

# Method 1: Typical - assumes current CPI continues
eac_typical <- eac(bac, method = "typical", cpi = cpi)
cat("EAC (typical method):", round(eac_typical, 2), "\n")

EAC (typical method): 180000


# Method 2: Atypical - assumes future work at planned rate
eac_atypical <- eac(bac, method = "atypical", ac = ac, ev = ev)
cat("EAC (atypical method):", round(eac_atypical, 2), "\n")

EAC (atypical method): 128000


# Method 3: Combined - considers both CPI and SPI
eac_combined <- eac(bac, method = "combined", cpi = cpi, ac = ac, ev = ev, spi = spi)
cat("EAC (combined method):", round(eac_combined, 2), "\n")

EAC (combined method): 196714.3

Calculate additional forecasting metrics:

# Estimate to Complete (remaining cost at current CPI)
etc_val <- etc(bac, ev, cpi)
cat("Estimate to Complete (ETC):", round(etc_val, 2), "\n")

Estimate to Complete (ETC): 117000


# Variance at Completion (expected budget variance)
vac_val <- vac(bac, eac_typical)
cat("Variance at Completion (VAC):", round(vac_val, 2), "\n")

Variance at Completion (VAC): -80000

cat("Project is expected to be", abs(round(vac_val, 2)), "over budget\n")

Project is expected to be 80000 over budget


# To-Complete Performance Index (required efficiency to meet BAC)
tcpi_val <- tcpi(bac, ev, ac)
cat("TCPI (to meet BAC):", round(tcpi_val, 2), "\n")

TCPI (to meet BAC): 1.76

cat("Must achieve", round(tcpi_val * 100, 1), "% efficiency on remaining work to meet budget\n")

Must achieve 175.7 % efficiency on remaining work to meet budget

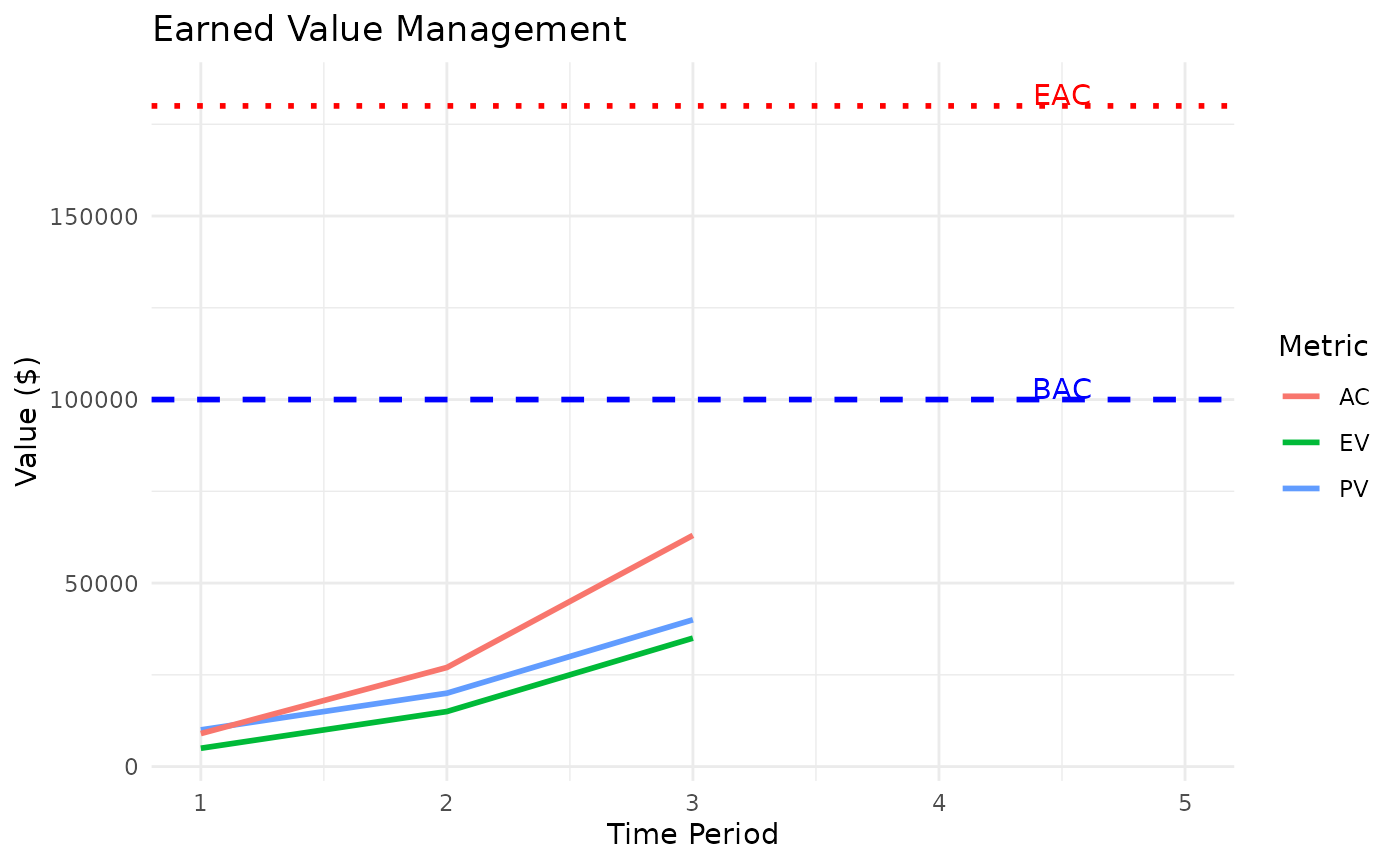
Finally, create a performance trend and plot the results:

# Calculate cumulative values for time periods 1 to 3
time_periods <- c(1, 2, 3)
actual_per_complete <- c(0.05, 0.15, 0.35)

# Calculate PV for each time period
pv_vals <- sapply(time_periods, function(t) pv(bac, schedule, t))

# Calculate cumulative AC for each time period
ac_vals <- cumsum(period_costs)

# Calculate EV for each time period
ev_vals <- sapply(actual_per_complete, function(a) ev(bac, a))

# Create a data frame for easier plotting
data <- data.frame(
  time_period = time_periods,
  PV = pv_vals,
  AC = ac_vals,
  EV = ev_vals
)

# Plot PV, AC, and EV over time
p <- ggplot2::ggplot(data, ggplot2::aes(x = time_period)) +
  ggplot2::geom_line(ggplot2::aes(y = PV, color = "PV"), linewidth = 1) +
  ggplot2::geom_line(ggplot2::aes(y = AC, color = "AC"), linewidth = 1) +
  ggplot2::geom_line(ggplot2::aes(y = EV, color = "EV"), linewidth = 1) +
  ggplot2::geom_hline(yintercept = bac, linetype = "dashed", color = "blue", linewidth = 1) +
  ggplot2::geom_hline(yintercept = eac_typical, linetype = "dotted", color = "red", linewidth = 1) +
  ggplot2::annotate("text", x = 4.5, y = bac + 3000, label = "BAC", color = "blue") +
  ggplot2::annotate("text", x = 4.5, y = eac_typical + 3000, label = "EAC", color = "red") +
  ggplot2::labs(
    title = "Earned Value Management",
    x = "Time Period",
    y = "Value ($)",
    color = "Metric"
  ) +
  ggplot2::xlim(1, 5) +
  ggplot2::theme_minimal()

# Print the plot
print(p)