Skip to contents

Monte Carlo Simulation.

Source: R/mcs.R
mcs.Rd

This function performs a Monte Carlo simulation to estimate the total duration of a project based on individual task distributions and an optional correlation matrix.

Usage

mcs(num_sims, task_dists, cor_mat = NULL)

Arguments

num_sims

The number of simulations to run.

task_dists

A list of lists describing each task distribution with its parameters. Each task distribution should be specified as a list with a "type" field (indicating the distribution type: "normal", "triangular", or "uniform") and the corresponding parameters: for "normal" (mean, sd), for "triangular" (a, b, c), and for "uniform" (min, max). For example: list( list(type = "normal", mean = 10, sd = 2), list(type = "triangular", a = 5, b = 10, c = 15), list(type = "uniform", min = 8, max = 12) )

cor_mat

The correlation matrix for the tasks (Optional). If not provided, tasks are assumed to be independent.

Value

The function returns a list of the total mean, variance, standard deviation, and percentiles for the project.

Note

When a correlation matrix is supplied, dependence is induced by Cholesky decomposition. The correlation matrix is factored, independent standard normal scores are multiplied by the Cholesky factor to carry the target correlation, and each column is then returned to its own scale through the normal CDF and that task's inverse CDF. Applying the factor to standard normal scores rather than to the raw task draws is required for the factorization to be valid, since it presumes unit-variance inputs. Every marginal distribution is therefore preserved exactly. The sampled rank correlation matches the target matrix, while the product-moment correlation is approximate: it is attenuated for strongly skewed marginals, an inherent property of the transform. smm() remains available when only first and second moments are needed; see the package's design-structure tools for modeling structural dependence directly.

References

Damnjanovic, Ivan, and Kenneth Reinschmidt. Data analytics for engineering and construction project risk management. No. 172534. Cham, Switzerland: Springer, 2020.

Examples

# Set the number of simulations and task distributions for a toy project.
num_sims <- 10000
task_dists <- list(
  list(type = "normal", mean = 10, sd = 2), # Task A: Normal distribution
  list(type = "triangular", a = 5, b = 10, c = 15), # Task B: Triangular distribution
  list(type = "uniform", min = 8, max = 12) # Task C: Uniform distribution
)

# Set the correlation matrix for the correlations between tasks.
cor_mat <- matrix(c(
  1, 0.5, 0.3,
  0.5, 1, 0.4,
  0.3, 0.4, 1
), nrow = 3, byrow = TRUE)

# Run the Monte Carlo sumulation and print the results.
results <- mcs(num_sims, task_dists, cor_mat)
cat("Mean Total Duration:", results$total_mean, "\n")
#> Mean Total Duration: 30.03153 
cat("Variance of Total Variance:", results$total_variance, "\n")
#> Variance of Total Variance: 16.95771 
cat("Standard Deviation of Total Duration:", results$total_sd, "\n")
#> Standard Deviation of Total Duration: 4.117973 
cat("5th Percentile:", results$percentiles[1], "\n")
#> 5th Percentile: 23.25509 
cat("Median (50th Percentile):", results$percentiles[2], "\n")
#> Median (50th Percentile): 29.9976 
cat("95th Percentile:", results$percentiles[3], "\n")
#> 95th Percentile: 36.80591 
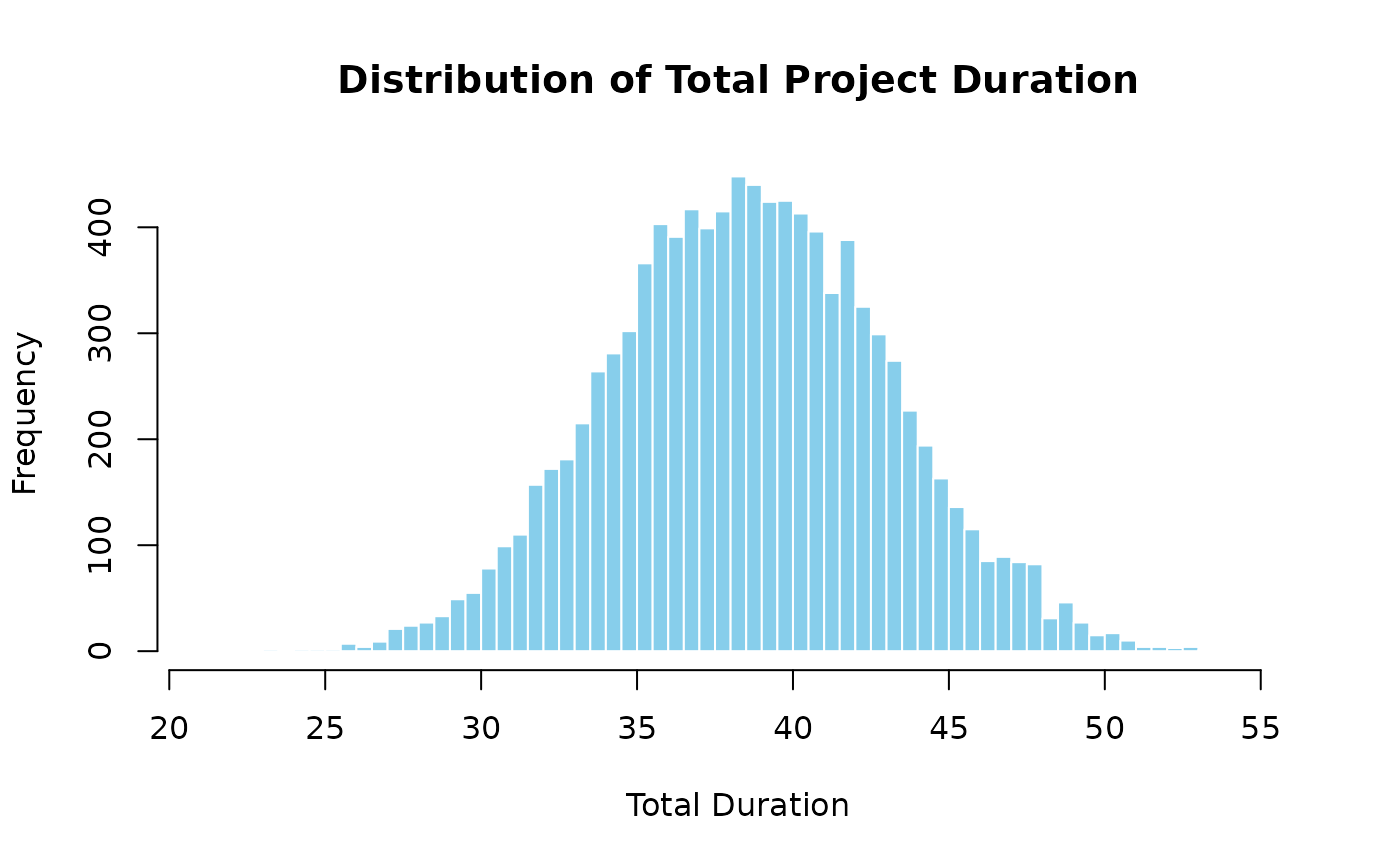
hist(results$total_distribution,
  breaks = 50, main = "Distribution of Total Project Duration",
  xlab = "Total Duration", col = "skyblue", border = "white"
)
legend("topright", legend = c("Total Duration Distribution"), fill = c("skyblue"))