Introduction
Similar to project-level risk analysis, Bayesian Networks are useful for analyzing project portfolio risks. Bayesian Networks are probabilistic graphical models that represent a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian Networks are helpful for modeling complex systems and making inferences about the relationships between variables.
Project Portfolio Risk Analysis
Imagine a simple project portfolio. The portfolio consists of 3 civil engineering projects: construction of a roadway, a small building construction, and a pedestrian bridge project. The primary tasks for these projects are as follows.
roadway_tasks <- data.frame(
ID = c("AF", "AG", "AH", "AI", "AJ", "AK", "AL", "AM"),
Label = c(
"Task-1.1",
"Task-1.2",
"Task-1.3",
"Task-1.4",
"Task-1.5",
"Task-1.6",
"Task-1.7",
"Task-1.8"
),
Task = c(
"Survey and Site Assessment",
"Design and Planning",
"Permitting and Approvals",
"Excavation and Grading",
"Pavement Installation",
"Drainage and Utilities Installation",
"Signage and Markings",
"Final Inspection and Handover"
),
Project_ID = rep("BF", 8)
)
knitr::kable(roadway_tasks, caption = "Project 1: Roadway Tasks")| ID | Label | Task | Project_ID |
|---|---|---|---|
| AF | Task-1.1 | Survey and Site Assessment | BF |
| AG | Task-1.2 | Design and Planning | BF |
| AH | Task-1.3 | Permitting and Approvals | BF |
| AI | Task-1.4 | Excavation and Grading | BF |
| AJ | Task-1.5 | Pavement Installation | BF |
| AK | Task-1.6 | Drainage and Utilities Installation | BF |
| AL | Task-1.7 | Signage and Markings | BF |
| AM | Task-1.8 | Final Inspection and Handover | BF |
building_tasks <- data.frame(
ID = c("AN", "AO", "AP", "AQ", "AR", "AS", "AT", "AU"),
Label = c(
"Task-2.1",
"Task-2.2",
"Task-2.3",
"Task-2.4",
"Task-2.5",
"Task-2.6",
"Task-2.7",
"Task-2.8"
),
Task = c(
"Architectural Design",
"Structural Engineering",
"Regulatory Approvals",
"Foundation and Excavation",
"Framing and Structural Work",
"Plumbing, Electrical, and HVAC Install",
"Interior and Exterior Finishing",
"Final Inspection and Handover"
),
Project_ID = rep("BG", 8)
)
knitr::kable(building_tasks, caption = "Project 2: Building Tasks")| ID | Label | Task | Project_ID |
|---|---|---|---|
| AN | Task-2.1 | Architectural Design | BG |
| AO | Task-2.2 | Structural Engineering | BG |
| AP | Task-2.3 | Regulatory Approvals | BG |
| AQ | Task-2.4 | Foundation and Excavation | BG |
| AR | Task-2.5 | Framing and Structural Work | BG |
| AS | Task-2.6 | Plumbing, Electrical, and HVAC Install | BG |
| AT | Task-2.7 | Interior and Exterior Finishing | BG |
| AU | Task-2.8 | Final Inspection and Handover | BG |
bridge_tasks <- data.frame(
ID = c("AV", "AW", "AX", "AY", "AZ", "BA", "BB", "BC", "BD", "BE"),
Label = c(
"Task-3.1",
"Task-3.2",
"Task-3.3",
"Task-3.4",
"Task-3.5",
"Task-3.6",
"Task-3.7",
"Task-3.8",
"Task-3.9",
"Task-3.10"
),
Task = c(
"Site Survey and Assessment",
"Environmental Impact Study",
"Concept Design and Planning",
"Structural Engineering and Analysis",
"Permitting and Approvals",
"Foundation and Pile Installation",
"Superstructure Construction",
"Decking and Surface Finishing",
"Inspection and Load Testing",
"Final Handover"
),
Project_ID = rep("BH", 10)
)
knitr::kable(bridge_tasks, caption = "Project 3: Bridge Tasks")| ID | Label | Task | Project_ID |
|---|---|---|---|
| AV | Task-3.1 | Site Survey and Assessment | BH |
| AW | Task-3.2 | Environmental Impact Study | BH |
| AX | Task-3.3 | Concept Design and Planning | BH |
| AY | Task-3.4 | Structural Engineering and Analysis | BH |
| AZ | Task-3.5 | Permitting and Approvals | BH |
| BA | Task-3.6 | Foundation and Pile Installation | BH |
| BB | Task-3.7 | Superstructure Construction | BH |
| BC | Task-3.8 | Decking and Surface Finishing | BH |
| BD | Task-3.9 | Inspection and Load Testing | BH |
| BE | Task-3.10 | Final Handover | BH |
Resources
Each project requires resources to complete the tasks. These resources are allocated to the tasks based on the project requirements. The resources for the projects are as follows.
roadway_resources <- data.frame(
ID = c("F", "G", "H", "I", "J", "K", "L", "M"),
Label = c(
"Resource-1.1",
"Resource-1.2",
"Resource-1.3",
"Resource-1.4",
"Resource-1.5",
"Resource-1.6",
"Resource-1.7",
"Resource-1.8"
),
Resource = c(
"Surveyer",
"Engineer",
"Regulatory Support",
"Heavy Machinery",
"Pavement and Related Machinery",
"Drainage Material and Equipment",
"Painters, Traffic Signs, Road Markers",
"Inspectors and Quality Control Support"
),
Task_ID = c("AF", "AG", "AH", "AI", "AJ", "AK", "AL", "AM"),
Task = c(
"Survey and Site Assessment",
"Design and Planning",
"Permitting and Approvals",
"Excavation and Grading",
"Pavement Installation",
"Drainage and Utilities Installation",
"Signage and Markings",
"Final Inspection and Handover"
),
Mean = c(
10000,
20000,
3500,
35000,
100000,
25000,
6500,
2000
),
SD = c(
2000,
5000,
1000,
10000,
20000,
5000,
1500,
500
)
)
knitr::kable(roadway_resources, caption = "Project 1: Roadway Resources")| ID | Label | Resource | Task_ID | Task | Mean | SD |
|---|---|---|---|---|---|---|
| F | Resource-1.1 | Surveyer | AF | Survey and Site Assessment | 10000 | 2000 |
| G | Resource-1.2 | Engineer | AG | Design and Planning | 20000 | 5000 |
| H | Resource-1.3 | Regulatory Support | AH | Permitting and Approvals | 3500 | 1000 |
| I | Resource-1.4 | Heavy Machinery | AI | Excavation and Grading | 35000 | 10000 |
| J | Resource-1.5 | Pavement and Related Machinery | AJ | Pavement Installation | 100000 | 20000 |
| K | Resource-1.6 | Drainage Material and Equipment | AK | Drainage and Utilities Installation | 25000 | 5000 |
| L | Resource-1.7 | Painters, Traffic Signs, Road Markers | AL | Signage and Markings | 6500 | 1500 |
| M | Resource-1.8 | Inspectors and Quality Control Support | AM | Final Inspection and Handover | 2000 | 500 |
building_resources <- data.frame(
ID = c("N", "O", "P", "Q", "R", "S", "T", "U"),
Label = c(
"Resource-2.1",
"Resource-2.2",
"Resource-2.3",
"Resource-2.4",
"Resource-2.5",
"Resource-2.6",
"Resource-2.7",
"Resource-2.8"
),
Resource = c(
"Architect",
"Structural Engineer",
"Regulatory Support",
"Heavy Machinery",
"Building Materials",
"Plumbers, Electricians",
"Painters, Interior Finishers",
"Inspector and Quality Control Support"
),
Task_ID = c("AN", "AO", "AP", "AQ", "AR", "AS", "AT", "AU"),
Task = c(
"Architectural Design",
"Structural Engineering",
"Regulatory Approvals",
"Foundation and Excavation",
"Framing and Structural Work",
"Plumbing, Electrical, and HVAC Install",
"Interior and Exterior Finishing",
"Final Inspection and Handover"
),
Mean = c(
15000,
30000,
4000,
40000,
100000,
20000,
8000,
2500
),
SD = c(
3000,
6000,
1000,
10000,
20000,
4000,
1500,
500
)
)
knitr::kable(building_resources, caption = "Project 2: Building Resources")| ID | Label | Resource | Task_ID | Task | Mean | SD |
|---|---|---|---|---|---|---|
| N | Resource-2.1 | Architect | AN | Architectural Design | 15000 | 3000 |
| O | Resource-2.2 | Structural Engineer | AO | Structural Engineering | 30000 | 6000 |
| P | Resource-2.3 | Regulatory Support | AP | Regulatory Approvals | 4000 | 1000 |
| Q | Resource-2.4 | Heavy Machinery | AQ | Foundation and Excavation | 40000 | 10000 |
| R | Resource-2.5 | Building Materials | AR | Framing and Structural Work | 100000 | 20000 |
| S | Resource-2.6 | Plumbers, Electricians | AS | Plumbing, Electrical, and HVAC Install | 20000 | 4000 |
| T | Resource-2.7 | Painters, Interior Finishers | AT | Interior and Exterior Finishing | 8000 | 1500 |
| U | Resource-2.8 | Inspector and Quality Control Support | AU | Final Inspection and Handover | 2500 | 500 |
bridge_resources <- data.frame(
ID = c("V", "W", "X", "Y", "Z", "AA", "AB", "AC", "AD", "AE"),
Label = c(
"Resource-3.1",
"Resource-3.2",
"Resource-3.3",
"Resource-3.4",
"Resource-3.5",
"Resource-3.6",
"Resource-3.7",
"Resource-3.8",
"Resource-3.9",
"Resource-3-10"
),
Resource = c(
"Surveyor",
"Environmental Scientist",
"Civil Engineer",
"Structural Engineer",
"Regulatory Consulting",
"Heavy Machinery",
"Steel and Concrete Materials",
"Decking Materials",
"Inspector and Quality Control Support",
"Handover Team"
),
Task_ID = c("AV", "AW", "AX", "AY", "AZ", "BA", "BB", "BC", "BD", "BE"),
Task = c(
"Site Survey and Assessment",
"Environmental Impact Study",
"Concept Design and Planning",
"Structural Engineering and Analysis",
"Permitting and Approvals",
"Foundation and Pile Installation",
"Superstructure Construction",
"Decking and Surface Finishing",
"Inspection and Load Testing",
"Final Handover"
),
Mean = c(
10000,
20000,
30000,
40000,
5000,
50000,
100000,
20000,
5000,
10000
),
SD = c(
2000,
4000,
6000,
8000,
1000,
10000,
20000,
4000,
1000,
2000
)
)
knitr::kable(bridge_resources, caption = "Project 3: Bridge Resources")| ID | Label | Resource | Task_ID | Task | Mean | SD |
|---|---|---|---|---|---|---|
| V | Resource-3.1 | Surveyor | AV | Site Survey and Assessment | 1e+04 | 2000 |
| W | Resource-3.2 | Environmental Scientist | AW | Environmental Impact Study | 2e+04 | 4000 |
| X | Resource-3.3 | Civil Engineer | AX | Concept Design and Planning | 3e+04 | 6000 |
| Y | Resource-3.4 | Structural Engineer | AY | Structural Engineering and Analysis | 4e+04 | 8000 |
| Z | Resource-3.5 | Regulatory Consulting | AZ | Permitting and Approvals | 5e+03 | 1000 |
| AA | Resource-3.6 | Heavy Machinery | BA | Foundation and Pile Installation | 5e+04 | 10000 |
| AB | Resource-3.7 | Steel and Concrete Materials | BB | Superstructure Construction | 1e+05 | 20000 |
| AC | Resource-3.8 | Decking Materials | BC | Decking and Surface Finishing | 2e+04 | 4000 |
| AD | Resource-3.9 | Inspector and Quality Control Support | BD | Inspection and Load Testing | 5e+03 | 1000 |
| AE | Resource-3-10 | Handover Team | BE | Final Handover | 1e+04 | 2000 |
Risks
Each project is also subject to risks that can impact the project outcomes. Each risk event has a probability of occurrence and an impact on the project. The risks for the projects are as follows.
roadway_risks <- data.frame(
Risk_ID = c("A", "B", "C"),
Name = c(
"Risk-1",
"Risk-2",
"Risk-3"
),
Risk = c(
"Delays in Permitting and Approvals",
"Unforeseen Site Conditions",
"Material Price Fluctuations"
),
Probability = c(
0.9,
0.95,
0.8
),
Resource_ID = c("H", "I", "J"),
Resource_Impacted = c(
"Regulatory Support",
"Heavy Machinery",
"Pavement and Related Machinery"
),
Mean = c(
7000,
70000,
200000
),
SD = c(
2000,
20000,
40000
)
)
knitr::kable(roadway_risks, caption = "Project 1: Roadway Risks")| Risk_ID | Name | Risk | Probability | Resource_ID | Resource_Impacted | Mean | SD |
|---|---|---|---|---|---|---|---|
| A | Risk-1 | Delays in Permitting and Approvals | 0.90 | H | Regulatory Support | 7e+03 | 2000 |
| B | Risk-2 | Unforeseen Site Conditions | 0.95 | I | Heavy Machinery | 7e+04 | 20000 |
| C | Risk-3 | Material Price Fluctuations | 0.80 | J | Pavement and Related Machinery | 2e+05 | 40000 |
building_risks <- data.frame(
Risk_ID = c("A", "D", "C"),
Name = c(
"Risk-1",
"Risk-4",
"Risk-3"
),
Risk = c(
"Delays in Permitting and Approvals",
"Labor Shortage or Skills Gap",
"Material Price Volatility"
),
Probability = c(
0.9,
0.9,
0.8
),
Resource_ID = c("P", "S", "O"),
Resource = c(
"Regulatory Support",
"Plumbers, Electricians",
"Building Materials"
),
Mean = c(
8000,
40000,
60000
),
SD = c(
2000,
8000,
12000
)
)
knitr::kable(building_risks, caption = "Project 2: Building Risks")| Risk_ID | Name | Risk | Probability | Resource_ID | Resource | Mean | SD |
|---|---|---|---|---|---|---|---|
| A | Risk-1 | Delays in Permitting and Approvals | 0.9 | P | Regulatory Support | 8000 | 2000 |
| D | Risk-4 | Labor Shortage or Skills Gap | 0.9 | S | Plumbers, Electricians | 40000 | 8000 |
| C | Risk-3 | Material Price Volatility | 0.8 | O | Building Materials | 60000 | 12000 |
bridge_risks <- data.frame(
Risk_ID = c("B", "D", "E"),
Name = c(
"Risk-2",
"Risk-4",
"Risk-5"
),
Risk = c(
"Unforeseen Environmental Conditions",
"Labor Supply Disruptions",
"Structural Design Revisions"
),
Probabiliy = c(
0.95,
0.9,
0.95
),
Resource_ID = c("W", "AD", "Y"),
Resource = c(
"Environmental Scientist",
"Inspector and Quality Control Support",
"Structural Engineer"
),
Mean = c(
40000,
10000,
80000
),
SD = c(
9000,
2000,
16000
)
)
knitr::kable(bridge_risks, caption = "Project 3: Bridge Risks")| Risk_ID | Name | Risk | Probabiliy | Resource_ID | Resource | Mean | SD |
|---|---|---|---|---|---|---|---|
| B | Risk-2 | Unforeseen Environmental Conditions | 0.95 | W | Environmental Scientist | 40000 | 9000 |
| D | Risk-4 | Labor Supply Disruptions | 0.90 | AD | Inspector and Quality Control Support | 10000 | 2000 |
| E | Risk-5 | Structural Design Revisions | 0.95 | Y | Structural Engineer | 80000 | 16000 |
Notice how the risks are associated with the resources. The risks can impact the resources, and the resources can ultimately impact the project outcomes. Most of the risks are also common across the projects. For example, Risk 1 is common across all three projects. If Risk 1 occurs, the impact will be felt across all three.
Bayesian Network
A Bayesian network is useful for modeling project portfolio risks. The Bayesian Network represents the dependencies between the projects, tasks, resources, and risks. The network helps in understanding the relationships between the variables and in making inferences about the risks.
First, define the nodes and edges of the Bayesian network. The nodes represent the variables, and the edges represent the dependencies between the variables. The following code defines the nodes and edges of the Bayesian network.
nodes <- data.frame(
id = c("A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N",
"O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z", "AA", "AB",
"AC", "AD", "AE", "AF", "AG", "AH", "AI", "AJ", "AK", "AL", "AM", "AN",
"AO", "AP", "AQ", "AR", "AS", "AT", "AU", "AV", "AW", "AX", "AY", "AZ",
"BA", "BB", "BC", "BD", "BE", "BF", "BG", "BH", "BI"),
label = c(
"Risk-1",
"Risk-2",
"Risk-3",
"Risk-4",
"Risk-5",
"Resource-1.1",
"Resource-1.2",
"Resource-1.3",
"Resource-1.4",
"Resource-1.5",
"Resource-1.6",
"Resource-1.7",
"Resource-1.8",
"Resource-2.1",
"Resource-2.2",
"Resource-2.3",
"Resource-2.4",
"Resource-2.5",
"Resource-2.6",
"Resource-2.7",
"Resource-2.8",
"Resource-3.1",
"Resource-3.2",
"Resource-3.3",
"Resource-3.4",
"Resource-3.5",
"Resource-3.6",
"Resource-3.7",
"Resource-3.8",
"Resource-3.9",
"Resource-3-10",
"Task-1.1",
"Task-1.2",
"Task-1.3",
"Task-1.4",
"Task-1.5",
"Task-1.6",
"Task-1.7",
"Task-1.8",
"Task-2.1",
"Task-2.2",
"Task-2.3",
"Task-2.4",
"Task-2.5",
"Task-2.6",
"Task-2.7",
"Task-2.8",
"Task-3.1",
"Task-3.2",
"Task-3.3",
"Task-3.4",
"Task-3.5",
"Task-3.6",
"Task-3.7",
"Task-3.8",
"Task-3.9",
"Task-3.10",
"Project 1",
"Project 2",
"Project 3",
"Project Portfolio"
),
group = c(
"Risk",
"Risk",
"Risk",
"Risk",
"Risk",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Resource",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Task",
"Project",
"Project",
"Project",
"Portfolio"
),
stringsAsFactors = FALSE
)Next, define the edges of the Bayesian network. The following code defines the edges of the Bayesian network.
links <- data.frame(
source = c("A", "B", "C", "A", "D", "C", "B", "D", "E", "F", "G", "H", "I",
"J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W",
"X", "Y", "Z", "AA", "AB", "AC", "AD", "AE", "AF", "AG", "AH", "AI",
"AJ", "AK", "AL", "AM", "AN", "AO", "AP", "AQ", "AR", "AS", "AT", "AU",
"AV", "AW", "AX", "AY", "AZ", "BA", "BB", "BC", "BD", "BE", "BF", "BG",
"BH"),
target = c("H", "I", "J", "P", "S", "O", "W", "AD", "Y", "AF", "AG", "AH", "AI",
"AJ", "AK", "AL", "AM", "AN", "AO", "AP", "AQ", "AR", "AS", "AT", "AU",
"AV", "AW", "AX", "AY", "AZ", "BA", "BB", "BC", "BD", "BE", "BF", "BF",
"BF", "BF", "BF", "BF", "BF", "BF", "BG", "BG", "BG", "BG", "BG", "BG",
"BG", "BG", "BH", "BH", "BH", "BH", "BH", "BH", "BH", "BH", "BH", "BH",
"BI", "BI", "BI"),
value = rep(1, 64)
)Then define the distributions for the nodes. The distributions represent the probabilities of the outcomes for each node. The following code defines the distributions for the nodes.
distributions <- list(
A = list(
type = "discrete",
values = c(1, 0),
probs = c(0.9, 0.1)
),
B = list(
type = "discrete",
values = c(1, 0),
probs = c(0.95, 0.05)
),
C = list(
type = "discrete",
values = c(1, 0),
probs = c(0.8, 0.2)
),
D = list(
type = "discrete",
values = c(1, 0),
probs = c(0.9, 0.1)
),
E = list(
type = "discrete",
values = c(1, 0),
probs = c(0.95, 0.05)
),
F = list(
type = "normal",
mean = 10000,
sd = 2000
),
G = list(
type = "normal",
mean = 20000,
sd = 5000
),
H = list(
type = "conditional",
condition = c("A"),
true_dist = list(
type = "normal",
mean = 7000,
sd = 2000
),
false_dist = list(
type = "normal",
mean = 3500,
sd = 1000
)
),
I = list(
type = "conditional",
condition = c("B"),
true_dist = list(
type = "normal",
mean = 70000,
sd = 20000
),
false_dist = list(
type = "normal",
mean = 35000,
sd = 10000
)
),
J = list(
type = "conditional",
condition = c("C"),
true_dist = list(
type = "normal",
mean = 100000,
sd = 40000
),
false_dist = list(
type = "normal",
mean = 50000,
sd = 20000
)
),
K = list(
type = "normal",
mean = 25000,
sd = 5000
),
L = list(
type = "normal",
mean = 6500,
sd = 1500
),
M = list(
type = "normal",
mean = 2000,
sd = 500
),
N = list(
type = "normal",
mean = 15000,
sd = 3000
),
O = list(
type = "conditional",
condition = c("C"),
true_dist = list(
type = "normal",
mean = 8000,
sd = 2000
),
false_dist = list(
type = "normal",
mean = 4000,
sd = 1000
)
),
P = list(
type = "conditional",
condition = c("A"),
true_dist = list(
type = "normal",
mean = 8000,
sd = 2000
),
false_dist = list(
type = "normal",
mean = 4000,
sd = 1000
)
),
Q = list(
type = "normal",
mean = 40000,
sd = 10000
),
R = list(
type = "normal",
mean = 100000,
sd = 20000
),
S = list(
type = "conditional",
condition = c("D"),
true_dist = list(
type = "normal",
mean = 16000,
sd = 4000
),
false_dist = list(
type = "normal",
mean = 8000,
sd = 2000
)
),
T = list(
type = "normal",
mean = 8000,
sd = 1500
),
U = list(
type = "normal",
mean = 2500,
sd = 500
),
V = list(
type = "normal",
mean = 10000,
sd = 2000
),
W = list(
type = "conditional",
condition = c("B"),
true_dist = list(
type = "normal",
mean = 60000,
sd = 4000
),
false_dist = list(
type = "normal",
mean = 30000,
sd = 2000
)
),
X = list(
type = "normal",
mean = 30000,
sd = 6000
),
Y = list(
type = "conditional",
condition = c("E"),
true_dist = list(
type = "normal",
mean = 20000,
sd = 2000
),
false_dist = list(
type = "normal",
mean = 10000,
sd = 1000
)
),
Z = list(
type = "normal",
mean = 5000,
sd = 1000
),
AA = list(
type = "normal",
mean = 50000,
sd = 10000
),
AB = list(
type = "normal",
mean = 100000,
sd = 20000
),
AC = list(
type = "normal",
mean = 20000,
sd = 4000
),
AD = list(
type = "conditional",
condition = c("D"),
true_dist = list(
type = "normal",
mean = 40000,
sd = 8000
),
false_dist = list(
type = "normal",
mean = 20000,
sd = 4000
)
),
AE = list(
type = "normal",
mean = 10000,
sd = 2000
),
AF = list(
type = "aggregate",
nodes = c("F")
),
AG = list(
type = "aggregate",
nodes = c("G")
),
AH = list(
type = "aggregate",
nodes = c("H")
),
AI = list(
type = "aggregate",
nodes = c("I")
),
AJ = list(
type = "aggregate",
nodes = c("J")
),
AK = list(
type = "aggregate",
nodes = c("K")
),
AL = list(
type = "aggregate",
nodes = c("L")
),
AM = list(
type = "aggregate",
nodes = c("M")
),
AN = list(
type = "aggregate",
nodes = c("N")
),
AO = list(
type = "aggregate",
nodes = c("O")
),
AP = list(
type = "aggregate",
nodes = c("P")
),
AQ = list(
type = "aggregate",
nodes = c("Q")
),
AR = list(
type = "aggregate",
nodes = c("R")
),
AS = list(
type = "aggregate",
nodes = c("S")
),
AT = list(
type = "aggregate",
nodes = c("T")
),
AU = list(
type = "aggregate",
nodes = c("U")
),
AV = list(
type = "aggregate",
nodes = c("V")
),
AW = list(
type = "aggregate",
nodes = c("W")
),
AX = list(
type = "aggregate",
nodes = c("X")
),
AY = list(
type = "aggregate",
nodes = c("Y")
),
AZ = list(
type = "aggregate",
nodes = c("Z")
),
BA = list(
type = "aggregate",
nodes = c("AA")
),
BB = list(
type = "aggregate",
nodes = c("AB")
),
BC = list(
type = "aggregate",
nodes = c("AC")
),
BD = list(
type = "aggregate",
nodes = c("AD")
),
BE = list(
type = "aggregate",
nodes = c("AE")
),
BF = list(
type = "aggregate",
nodes = c("AF", "AG", "AH", "AI", "AJ", "AK", "AL", "AM")
),
BG = list(
type = "aggregate",
nodes = c("AN", "AO", "AP", "AQ", "AR", "AS", "AT", "AU")
),
BH = list(
type = "aggregate",
nodes = c("AV", "AW", "AX", "AY", "AZ", "BA", "BB", "BC", "BD", "BE")
),
BI = list(
type = "aggregate",
nodes = c("BF", "BG", "BH")
)
)Finally, define the Bayesian network using the nodes, edges, and distributions. The following code defines the Bayesian network.
The Bayesian network can be visualized using the igraph and networkD3 packages. The igraph package provides functions for creating and analyzing graph structures, and the networkD3 package provides functions for creating interactive network visualizations.
library(igraph)
library(networkD3)
g <- graph_from_data_frame(graph$links, vertices = graph$nodes, directed = TRUE)
d3g <- igraph_to_networkD3(g, group = graph$nodes$group)
forceNetwork(Links = d3g$links, Nodes = d3g$nodes, NodeID = "name", Group = "group", Value = "value",
zoom = TRUE, legend = TRUE, arrows = TRUE, opacity = 0.8, fontSize = 14)Inference
To analyze the Bayesian network, use probabilistic inference to calculate the probabilities of different outcomes. Probabilistic inference is the process of estimating the probability distribution of a variable given evidence about other variables. Inference helps in making predictions about the risks based on the observed data.
simulation_results <- prob_net_sim(graph, num_samples = 1000)The simulation results can be used to estimate the total project portfolio cost and assess the impact of risks on the project outcomes. The following code estimates the total portfolio cost.
hist <- hist(simulation_results$BI, breaks = 50, plot = FALSE)
plot(hist, main = "Total Project Portfolio Cost", xlab = "Project Cost", col = "skyblue", border = "white")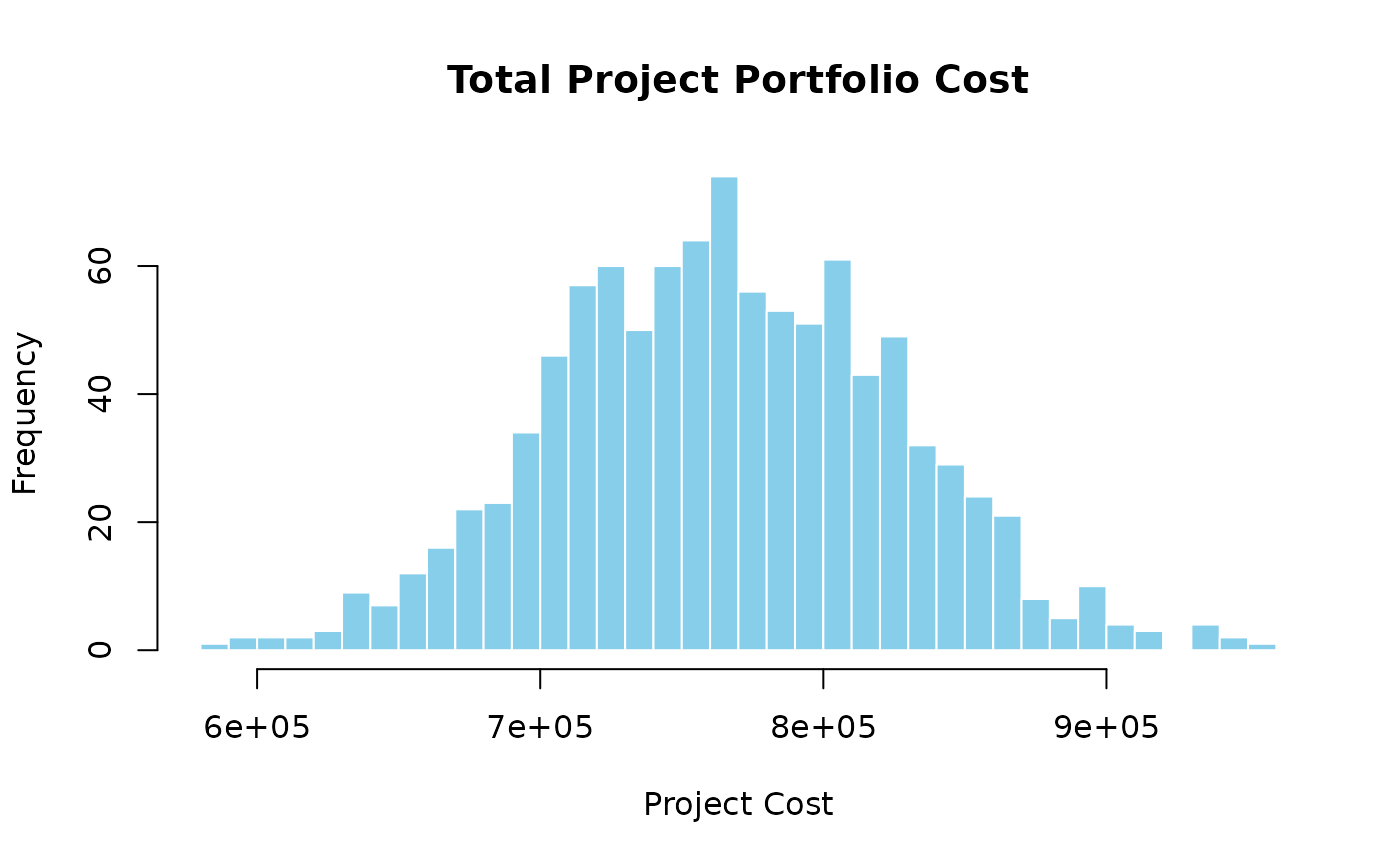
The histogram shows the distribution of the total portfolio cost. The histogram helps in understanding the range of possible project costs and assess the impact of risks on the project outcomes.
Learning
The Bayesian network can be updated with new data to improve the model’s accuracy. Learning the Bayesian network involves updating the distributions based on new evidence. The updated Bayesian network can be used to make more accurate predictions about the risks.
For example, if Risk 1.2 occurred, the Bayesian network can be updated with this new data. The following code updates the Bayesian network with the new data.
updated_results <- prob_net_learn(graph, observations = list(B = "Yes"),
num_samples = 1000)The updated results can be compared with the original results to see how the changes in the risk probabilities affect the project outcomes. The following code compares the results before and after updating the Bayesian network.
hist <- hist(simulation_results$I, breaks = 50, plot = FALSE)
hist2 <- hist(updated_results$I, breaks = 50, plot = FALSE)
plot(hist, main = "Heavy Machinery Cost", xlab = "Resource Cost",
col = "skyblue", border = "white")
plot(hist2, col = "blue", border = "white", add = TRUE)
legend("topright", legend = c("Before Update", "After Update"),
fill = c("skyblue", "blue"), bty = "n")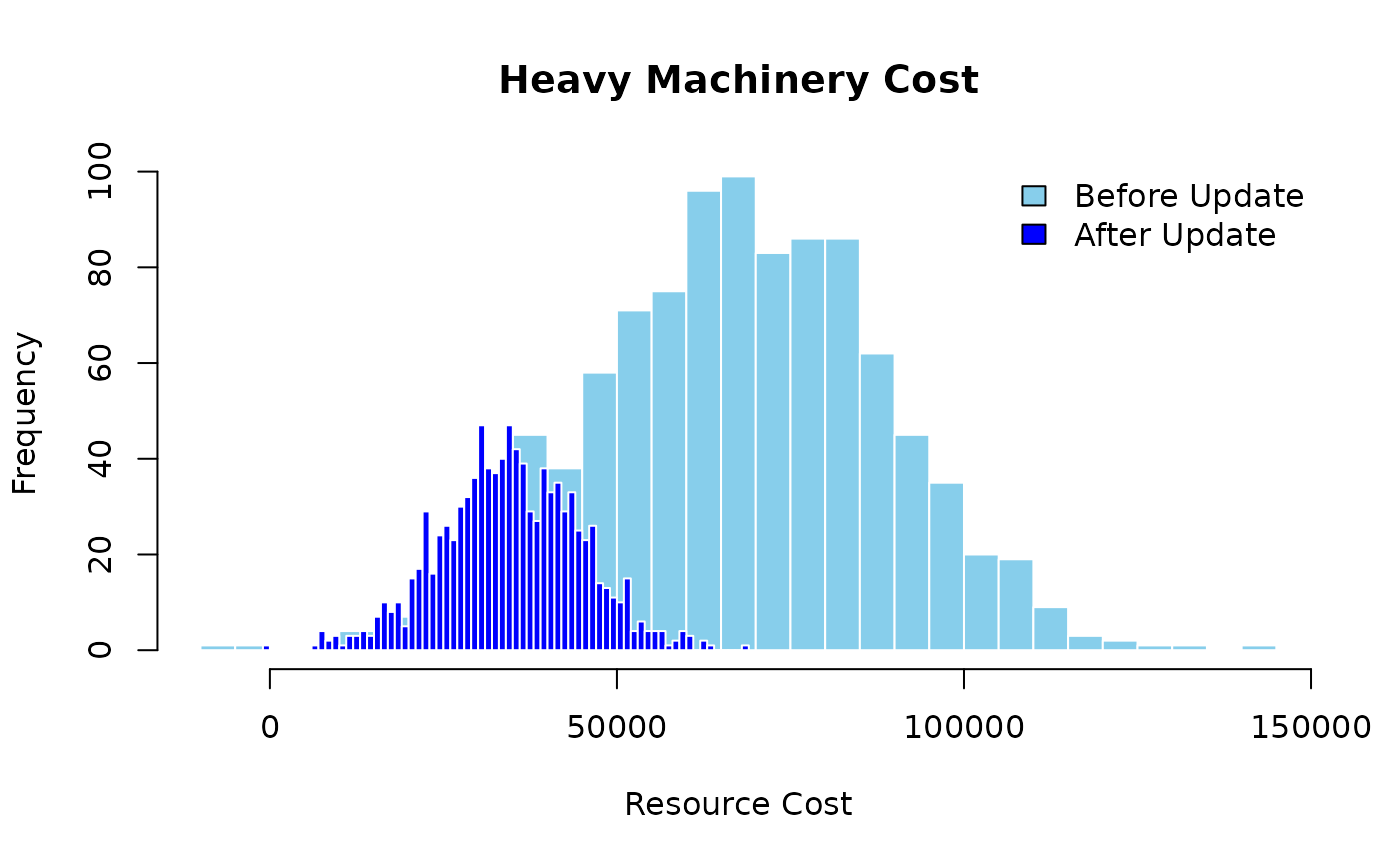
Updating
Similarly, the Bayesian network can be updated by adding or removing arcs between nodes. Adding or removing arcs changes the dependencies between the variables and improve the model’s accuracy.
For example, suppose Resource 1.3 is no longer at risk of delays. Remove the arc between Resource 1.3 and Risk 1.1 to account for this new information. The following code removes the arc between Resource 1.3 and Risk 1.1.
remove_links <- data.frame(
source = c("A"),
target = c("H"),
stringsAsFactors = FALSE
)
update_distributions <- list(
H = list(
type = "normal",
mean = 3500,
sd = 1000
)
)
updated_graph <- prob_net_update(graph, remove_links = remove_links,
update_distributions = update_distributions)
updated_results <- prob_net_sim(updated_graph, num_samples = 1000)Just as before, the updated results can be compared with the original results to see how the changes in the network structure affect the project outcomes.
hist <- hist(simulation_results$H, breaks = 50, plot = FALSE)
hist2 <- hist(updated_results$H, breaks = 50, plot = FALSE)
plot(hist, main = "Regulatory Support Cost", xlab = "Resource Cost",
col = "skyblue", border = "white", ylim = c(0, max(hist$counts, hist2$counts)))
plot(hist2, col = "blue", border = "white", add = TRUE)
legend("topright", legend = c("Before Update", "After Update"),
fill = c("skyblue", "blue"), bty = "n")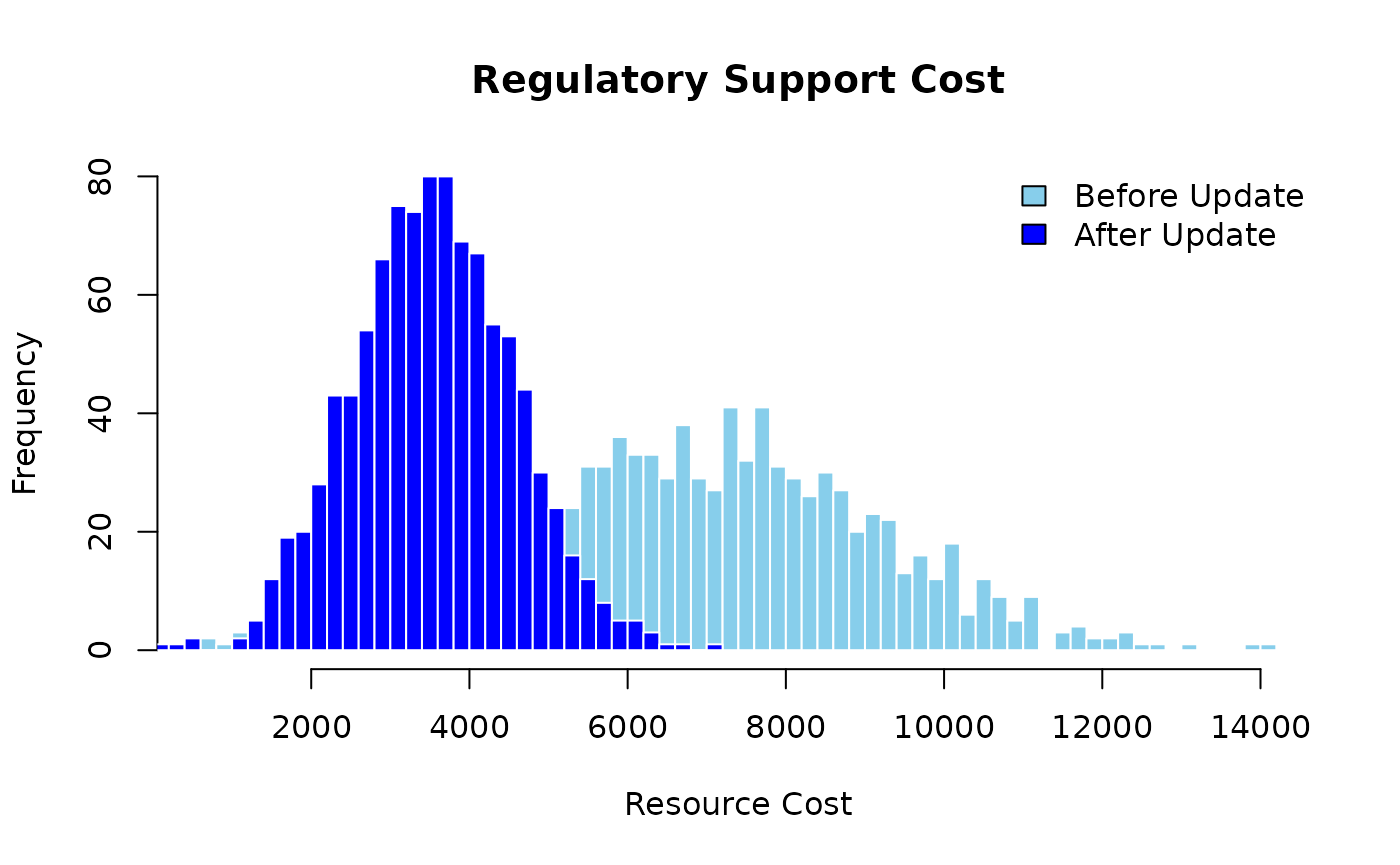
Conclusion
In this vignette, Bayesian Networks were used to analyze project portfolio risks. The projects, tasks, resources, and risks for a simple project portfolio were defined. A Bayesian network was then constructed to represent the dependencies between the variables. Probabilistic inference was applied to assess the risks and estimate the total project cost. The Bayesian network was also updated with new data to improve the model’s accuracy. Overall, the Bayesian network served as a powerful tool for modeling project portfolio risks and supporting informed decision-making regarding project outcomes.